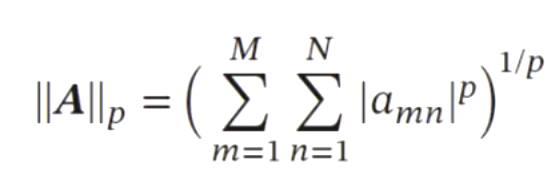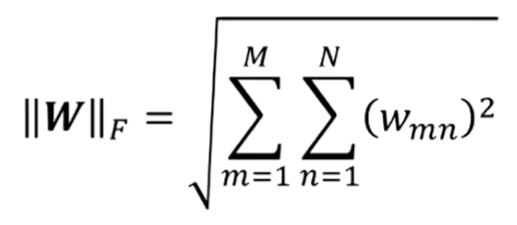深度学习课程笔记（一）：基础知识

这份笔记使用的部分图片、内容来自于北京交通大学深度学习课程，版权归课题组和原作者所有。

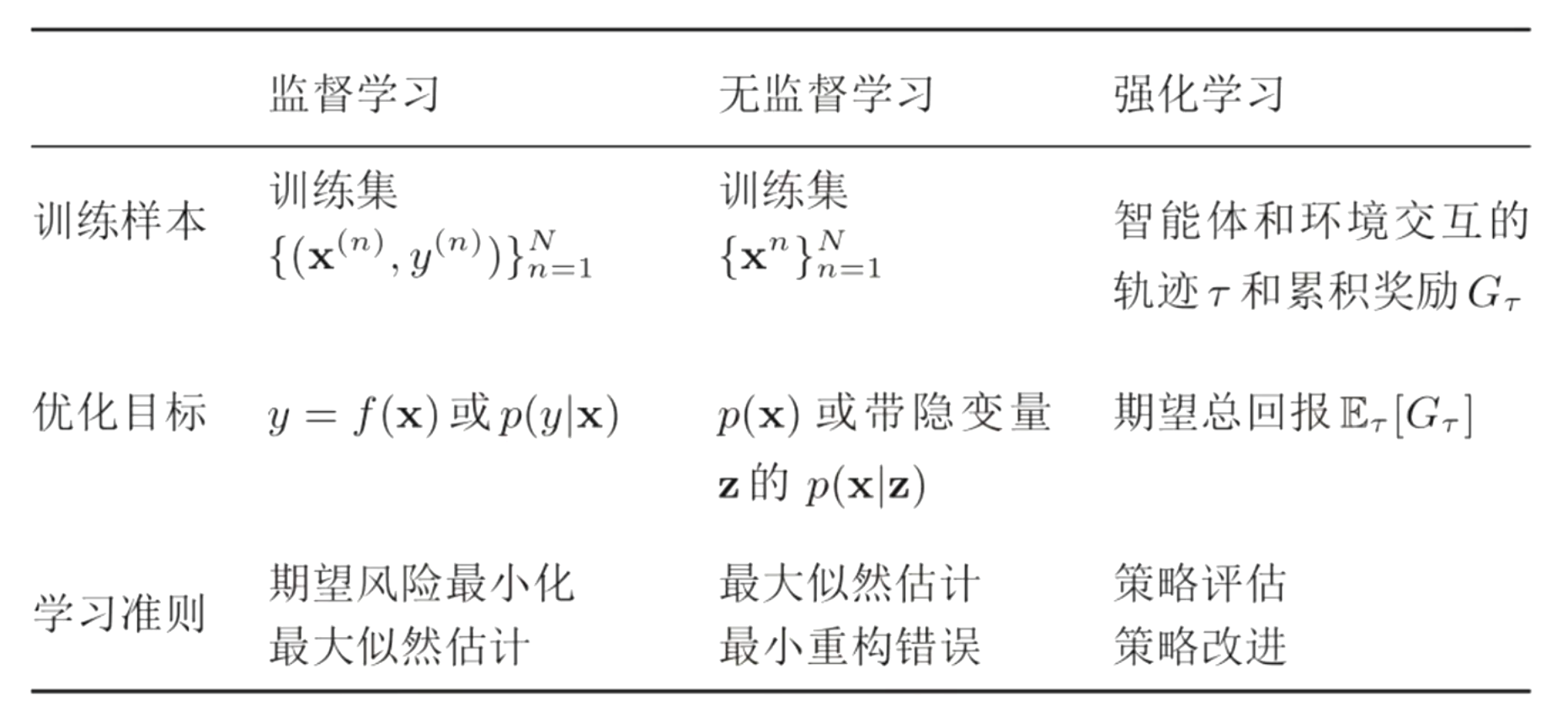
机器学习基础概念

1. 机器学习算法分类

数学基础

1. 范数：一个表示向量长度的函数

   • \(l_1\) 范数：向量的各个元素的绝对值之和

   • \(l_2\) 范数：向量的各个元素的平方和再开平方

   • \(l_\infin\) 范数：向量的各个元素的最大绝对值

   • 矩阵的范数

     • 常用的 \(l_p\) 范数

       

     • 矩阵的F范数是向量的l2范数的推广

       

2. 矩阵微分：多元微积分的一种表达方式，即使用矩阵和向量来表示因变量每个成分关于 自变量每个成分的偏导数

   • 分母布局

   

线性模型

深度学习除了最后一层，前面的N-1层都是在做特征变换（特征表示），只有最后一层在完成真正的任务（回归、分类）。

• 线性回归：输出的标签是连续值
• Logistic回归：二分类
• Softmax回归：多分类（三分类以上）
• 感知机

Logistic回归

将分类决策问题看作条件概率估计问题

• 用线性函数组合特征：\(f=w^Tx\)

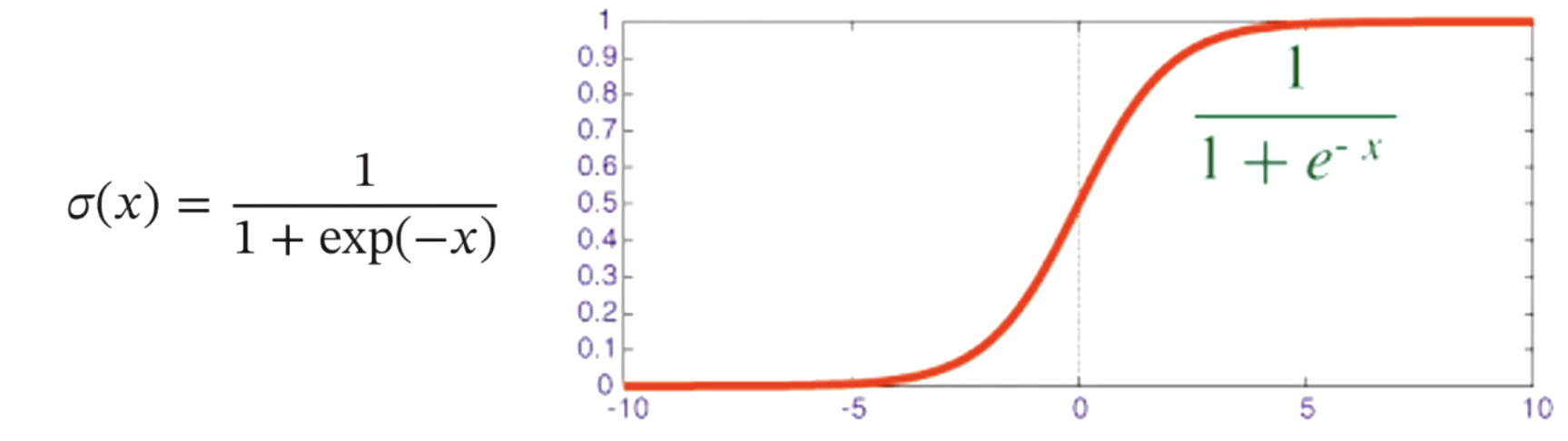
• 引入非线性函数 \(g(\cdot)\) 来计算类别标签的条件概率 $$p(y=c

  x)\(，其中\)c \in { 0,1 }$$

• 函数 \(g(\cdot)\) 把线性函数的值域从实数区间“挤压”到了 \((0,1)\) 之间，可以用来表示概率

如何构造 \(g(\cdot)\)：选择Logistic函数（激活函数）

• Logistic 回归可以看作预测值为“标签的对数几率”的线性回归模型。因此 Logistic 回归也称为对数几率回归（Logit Regression）

熵（Entropy）

在信息论中，熵用来衡量一个随机事件的不确定性

• 自信息（Self Information）：\(I(x)=-\log(p(x))\)
• 熵：自信息的期望

\[\begin{aligned} H(X) &= \mathbb{E}_X[I(x)] \\ &= \mathbb{E}_X[-\log p(x)] \\ &= -\sum_{x \in \mathcal{X}} p(x) \log p(x) \end{aligned}\]

熵越高，则随机变量的信息越多；熵越低，则随机变量的信息越少

在对分布 \(p(x)\) 的信息进行编码时，熵 \(H(p)\) 也是理论上最优的平均编码长 度，这种编码方式称为熵编码（Entropy Encoding）

例如：单选题有ABCD选项，每个概率为0.25，则 \(p(x)=0.25\)，代入得\(H(X)=2\)，符合ABCD使用2位进行编码：00 01 10 11

交叉熵（Cross Entropy）损失函数

交叉熵是按照概率分布α的最优编码对真实分布为p的信息进行编码的长度

\[\begin{aligned} H(p,q) &= \mathbb{E}_p[-\log q(x)] \\ &= -\sum_{x} p(x) \log q(x) \end{aligned}\]

• 在给定 p 的情况下，如果 q 和 p 越接近，交叉熵越小
• 如果 q 和 p 差别越大，交叉熵就越大

逻辑回归使用交叉作为损失函数

\[H(p,q) = -\sum_{x} p(x) \log q(x)\]

对于训练样本 \((x^{(n)}, y^{(n)})\)：

\[p_r(y^{(n)}=1|x^{(n)})=y^{(n)}, p_r(y^{(n)}=0|x^{(n)})=1-y^{(n)}\]

真实概率和预测概率之间的交叉熵为：

\[H(p,q) = -[p_r(y^{(n)}=1|x^{(n)})\log \hat y^{(n)}+p_r(y^{(n)}=0|x^{(n)})\log (1-\hat y^{(n)})\]

其中 \(\hat{y}^{(n)} = \sigma(w^\top x^{(n)})\)

Softmax 回归

Softmax Regression，也称为多项（Multinomial）或多类(Multi-Class）的Logistic 回归，是Logistic 回归在多分类问题上的推广。

Softmax 回归中，首先还是利用线性函数作特征的映射（判别函数），然后利用Softmax 函数作为非线性的决策函数

\[\begin{aligned} p(y=c|x)&=\mathrm{softmax}(w_c^\top x) \\ &=\frac{\exp(w_c^\top x)}{\sum_{c'=1}^C \exp(w_c^\top x)} \end{aligned}\] \[\begin{aligned} \hat y &= \arg \max_{c=1}^C p(y=c|x) \\ &= \arg \max_{c=1}^C w_c^\top x \end{aligned}\]

感知机（Perceptron）

感知机由Frank Rosenblatt于1958年提出，是一种广泛使用的线性分类器。感知器可谓是最简单的人工神经网络，只有一个神经元。

• 一种错误驱动的在线学习算法
• 先初始化一个权重向量 \(w \leftarrow 0\)（通常是全零向量）；
• 每次分错一个样本(x,y)时，即 \(yw^\top x <0\)
• 用这个样本来更新权重 \(w \leftarrow w+yx\)
• 根据感知器的学习策略，可以反推出感知器的损失函数为

\[\mathcal{L}({w}; {x}, y) = \max(0, -y {w}^\top {x})\]

小结

• 在 Logistic 回归和 Softmax 回归中，y 为类别的 one-hot 向量表示
• 在感知器中，\(y \in \{+1,-1\}\)